lkpcustomer.blogg.se - How to find z score on ti nspire

Note that 75% of the data would fall ABOVE this score and 75% of the area under the curve would be to the RIGHT of this z-score. 25% of the data would fall below this score and 25% of the area under the curve would be to the left of this z-score.

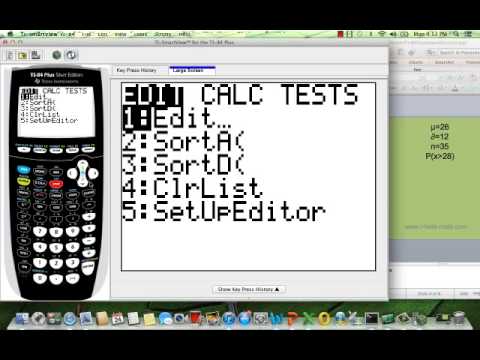
InvNorm() This invNorm(.25) function would return the z-score associated with the 25th percentile. The default is to use the standard normal distribution – and to return a z-score

Note: When you want the Raw score, enter values for mean and standard deviation. 90% of the data would fall below this score and 90% of the area under the curve would be to the left of this Raw score. InvNorm() This invNorm() function would return the score associated with the 90th percentile. Like normalcdf( L,H), invNorm(p) uses a default mean of zero and standard deviation of one: for the standard normal distribution. Inverse: invNorm() The Inverse Function While normalcdf( L,H,s) returns an area or probability given a Low and High bound, the inverse function: invNorm(p,s) returns a High bound when given a probability. (Total probability = 100%) OR use any z-score ABOVE 3.5 as the upper bound: Normalcdf(0.8, 5) Would return the area ABOVE z=0.8, which is The area Above the raw score of 112. Since there is very little data more than 3.5 standard deviations below the mean, use any z-score below -3.5 as the low bound: Normalcdf(-5,0.8) Would return the area below z=0.8, which is The area below the raw score of 112.Ībove a z-score To find the area ABOVE 112, you could subtract the area below 112 from 1. The z-score based on a raw score of 112 for a distribution that has a mean of 100 and a standard deviation of 15would be: = 0.8īetween 2 z-scores The normalcdf function defaults to a mean of zero and a standard deviation of one: these are the parameters for the standard normal distribution.īetween 2 z-scores This would return the area under a standard normal curve between the z-scores of -1.5 and 2.īelow a z-score Another way to find the cumulative area for scores below 112, would be to first convert to a z-score: = 0.8 Find the area in the standard normal distribution. Z-scores A standard or z-score measures the distance between each item and the mean in terms of the number of standard deviations.

This would return the area under a normal curve below 112 (to the left).

This would return the area under a normal curve between 112 and 122 for a distribution that has a mean of 100 and a standard deviation of 15.

Normalpdf( height of the curve The TI-83 provides three functions for Normal Distribution: normalcdf( area under the curve invNorm( score associated with the given areaĪrea or Probability Area under the Curvenormalcdf(low, high, mean, stdev)Returns the area under the curve (aka: probability, relative frequency)between the low and high scores. To access the TI-83 functions for Normal DistributionsPress 2ndand VARS

Normal Distributionusing the TI-83 Graphing Calculator